曲面方程
一、球面方程
球心位于$(a,b,c)$,半径为$R$的球面方程为:
$(x-a)^2+(y-b)^2+(z-c)^2=R^2$
二、旋转曲面
曲线$C$绕$z$轴旋转形成的曲面方程为:$f(y,z)=0$
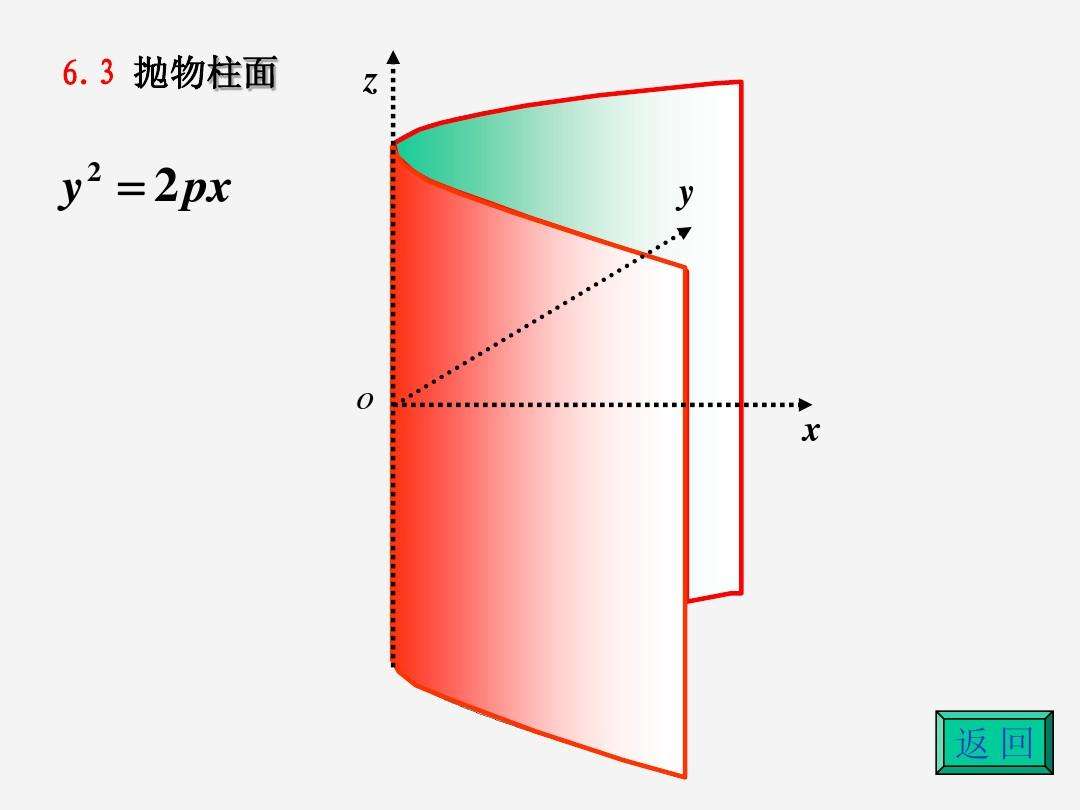
三、柱面
$x^2+y^2=R^2$
$y^2=2x$
四、二次曲面
1.椭圆锥面
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=z^2$
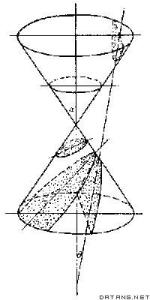
使用平面$z=t$截此曲面,$t=0$时得到一点$(0,0,0,)$。$t\neq 0$时得到:
$\frac{x^2}{(at)^2}+\frac{y^2}{(bt)^2}=1$
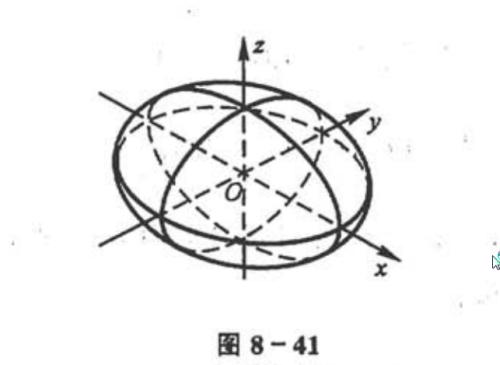
2.椭球面
$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
当$a=b=c$时,椭球面变为球面。
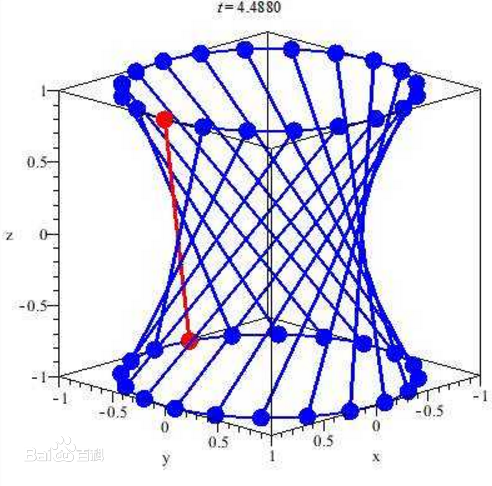
3.单叶双曲面
$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$
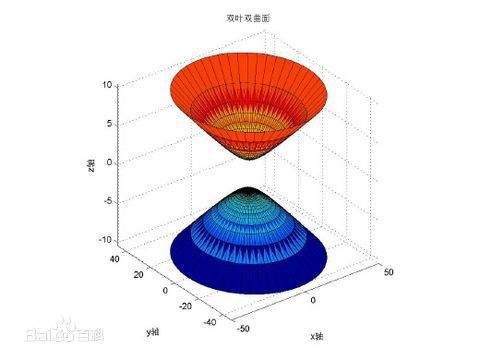
4.双叶双曲面
$\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$
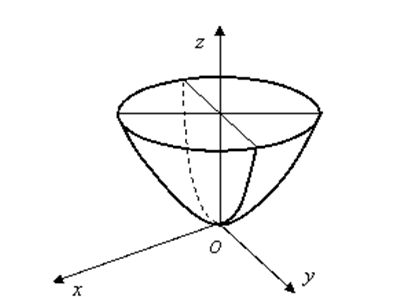
5.椭圆抛物面
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=z$
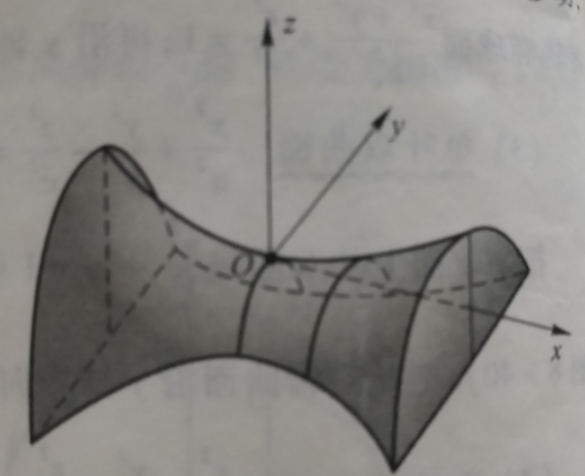
6.双曲抛物面(马鞍面)
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=z$
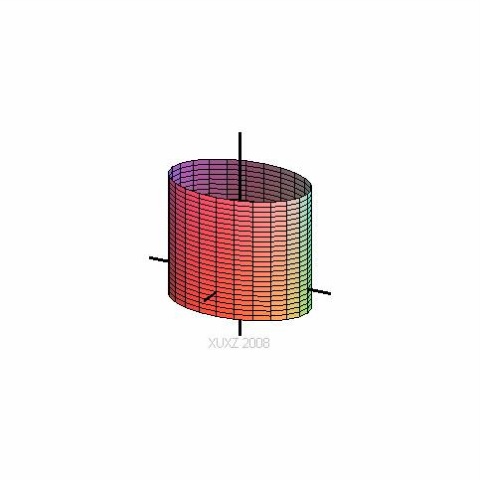
7.椭圆柱面
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

8.双曲柱面
$\frac{x^2}{a^2}-\frac{x^2}{b^2}=1$
9.抛物柱面
$x^2=ay$